I stumbled upon an old tweet by Vitalik Buterin (the creator of Ethereum) a few days ago, and got really confused.
Actually, 'baffled' is more like it.
The tweet wasn't an actual tweet... it was a poll.
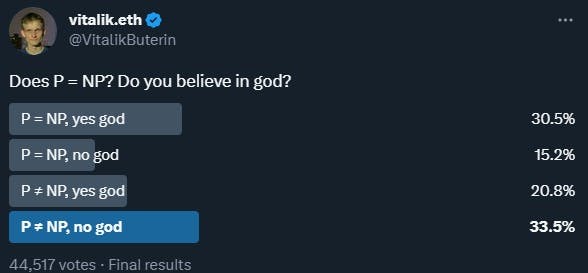
Doesn't seem very confusing, does it?
Okay, maybe it is.
P stands for 'pizza', and NP stands for 'not pizza'. Therefore, P != NP means pizza doesn't equal 'Not-Pizza'.
Right?
I didn't get the "god" bit though.
I was sure I'd have something to say about Buterin's poll... if I understood what P != NP really meant.
And as the curious, rest-hating person I've always been, I grabbed a shovel, went digging, and found out some very interesting things.
Now, I realize that not everyone who gets to read this might enjoy jargon-infused articles about complicated subjects. So I'll try to cut back on the 'sciencey' stuff, and explain the things I found as simply as I can.
Back to the P = NP issue.
P as you might have guessed, isn't pizza. And NP isn't 'not-pizza'. They'd be a lot more fun if they were though.
These two sides of the 'equation' form one of the most popular unsolved questions in theoretical computer science (I had no idea there was anything like 'theoretical' computer science to begin with).
Makes you wonder if 'theoretical biology' is, or will ever be an actual thing.
Anyway, the P versus NP problem is one of the most intriguing and fundamental problems in computer science today. In essence, this problem asks: "If the solution to a problem is easy to VERIFY, does that mean that its solution is easy to FIND as well?"

This may seem like a simple question... Scratch that.
It's still very confusing.
However, what you should know is that the implications of solving this problem are very important, and have been significant since they came to light in the 1970s.
Just keep reading. Because what you are about to read is an exploration of the P versus NP dilemma.
I assure you, this MIGHT interest you.
Oh, and about the weird a** title... "Wahala" is a Nigerian pidgin word meaning "problem".
Now that that's out of the way, let's explore:
P Versus NP: P Problems
First, let's start with some basic definitions. The "P" part of the P versus NP problem stands for problems that can be solved "quickly".
Keep in mind that I use the word "quickly" very loosely here.
A problem that takes years to solve may still be referred to as "quickly" solved.
Anyway, P problems are problems that can be solved in a reasonable amount of time, even as the size of the problem grows.
Don't worry, I'm not about to start a full craze-episode, trying to explain the concept of time complexity in algorithms.
Keeping that in mind, I'll try to include illustrations and examples as I go along. And since I promised to cut back on the 'sciencey' stuff, we can visit algorithmic time complexity in another article.
At the same time, a basic grasp of this concept can be beneficial, if you intend to understand the rest of this article.
An example, shall we?
If I gave you a scrambled list of numbers containing digits from 1 - 20, and then I asked you to find the number 20, in exchange for a 1000 Naira bill.
You'd probably accept my challenge.
What you'd most likely do is scan through the list from top to bottom, moving on when your eyes rest on a digit that isn't 20. Eventually, you'll find my digit, show it to me, and receive your cash.

If the number 20 happens to be the last number on the list, you'd have scanned my list digit by digit, 20 times until you found it... The 'worst case' time complexity of your algorithm would be 20 in this case (because you'd have scanned 20 times at most).
Some problems in computer science (and a million other fields) have been demonstrated as being solvable in polynomial time (a figure N^x, in which N is the number of inputs).
If the time complexity of your approach to the list when I offered you the 1000 Naira note was N, the value of N would be 40 at most if I gave you 40 numbers to scan, and 80 at most if I gave you 80 numbers.
Problems like these... problems shown to be solvable in polynomial time, reside in the class P.
P problems in general, refer to problems that can be solved in a reasonable amount of time.
NP problems, however, are problematic problems.
P Versus NP: NP Problems
The "NP" part of the problem stands for problems that are harder to solve and can't be solved "quickly".
There is no known way to tell if an NP problem can be solved reasonably as quickly as it can be verified.
If someone offered you a solution to an NP problem, however, you'd be able to tell in a reasonable amount of time, if they were right or if they were full of sh*t.
Like the solution to a quadratic equation that can be verified by substituting the values of X, and seeing if the equation equals zero. Keep in mind that this is only an illustration.
Quadratic equations are "very P".
The point is that NP problems are problems that require a lot of time and computational power to solve, especially as the size of the input grows.
A good example is that of a Rubik's cube.
A 2x2 Rubik's cube can be scrambled into about 3,674,160 configurations, and solving it is doable.
A regular 3x3 cube on the other hand, can be scrambled into over 43 quintillion possible configurations, and can STILL be solved in a fairly reasonable amount of time.
That's just mad, isn't it?
However, you might find it easier to agree with me that a Rubik's cube becomes harder and harder to solve, the bigger it gets.

I'd like to see even the most powerful supercomputer take on a billion x billion Rubik's cube.
The point is that a Rubik's cube is both a P and NP problem. It is one of those problems that gravitates from P to NP, the greater the number of inputs it gets.
Is P = NP?
Here's where things start to get interesting. The question that the P versus NP problem asks, is whether there is an easy way to solve the hard problems as quickly as the easy ones.
In other words, is there a way to solve an NP problem as quickly as a P problem?
Is there an algorithm that can reduce NP problems into P problems, effectively making a 1,000,000,000 x 1,000,000,000 Rubik's cube relatively as easy to solve as a 3x3 cube?

This is an important question, because if we could create an algorithm capable of breaking down ANY hard question into a series of small ones that can be solved easily and quickly, it would have a big impact on many fields like cryptography and optimization as I plan to expain soon.
Unfortunately, despite tons of research, no one has been able to prove for sure whether it's possible or not.
In fact, the P versus NP problem is one of the Clay Mathematics Institute's seven Millennium Prize Problems, which are some of the most challenging problems in mathematics today.
Whoever demonstrates the reduction of NP problems into P problems gets a whopping one million dollars.
How Crazy Would P = NP Be?
Very Crazy indeed.
Not to be a pessimist, but asides the millions of years in technological advances we could make with such an algorithm, a lot of things would also go up in flames.
For example, many encryption algorithms rely on the fact that certain problems are hard to solve, such as factoring large numbers into their prime factors.
In essence, the bitcoin or Ether in your wallet is only safe because P currently doesn't equal NP.
If NP is finally proven to be reducible to P and an algorithm that does just that is created, your private keys can (and will) be "de-hashed", leaving your precious coins vulnerable to theft.

Our idea of "cybersecurity" would go right down the drain, leaving governments, individuals' personal information and yes, nuclear codes and so much more, vulnerable to attack and theft.
Enough of the doom and gloom though.
P being equal to NP would also open up a whole new perspective of problem-solving.
Faster pocket computers taking seconds to calculate the shortest distance between two points in the observable universe, a cure for cancer (and basically every other kind of disease), interplanetary colonization, or even an over-the counter cure to aging itself.
We would jump thousands of years into the future in terms of technological advancement, and maybe even crack the problem of time travel and deep space exploration (among a million other problems).
At the same time, P = NP might also open up a world of unforeseen calamity and wonder.
For example, some people have argued that P = NP has implications for the nature of reality itself.
The idea is that if P equals NP, it could mean that the universe is indeed a simulation, since it would mean that complex problems could be solved quickly and efficiently.
Of course, this is just speculation, but it's a testament to the far-reaching implications of the P versus NP problem.
What If P != NP?
On the other hand, if P != NP (which it still is), there remain limits to what we can do with computers.
Your crypto is safe, and your Facebook account is still reasonably hard to hack.
In the meantime, the P versus NP problem continues to fascinate and inspire researchers and the public alike. It's a problem that touches on many important questions, such as the limits of computation, the nature of reality, and the power of human ingenuity.
